 |
SESIÓN
DE APRENDIZAJE N° 23
ÁREA DE MATEMÁTICA
SEGUNDO: A - B - C - D – E – F.
DOCENTES: CABELLO MELO, MAURO
RAMOS FLORES, JESSICA
SEMANA: 24
Competencia:
Resuelve problemas de regularidad,
equivalencia y cambio.
PROPÓSITO: Aprendemos a reconocer los elementos y propiedades
de ecuaciones e inecuaciones de primer grado a través diagramas para poder
desarrollar los problemas.
TÍTULO
DE LA SESIÓN
RECONOCEMOS LOS
ELEMENTOS Y PROPIEDADES DE ECUACIONES E INECUACIONES DE PRIMER GRADO EN
SITUACIONES DEL CONTEXTO REAL
RECOMENDACIONES:
Frenar el avance de la enfermedad del
coronavirus está en nuestras manos, no te olvides de seguir las recomendaciones
que el gobierno nos da y respetemos el aislamiento social sin olvidarnos de
practicar las normas de convivencia en casa y en las clases.
¿CÓMO EMPEZAMOS?
Buenos días
mis estimados estudiantes, felicitarle a cada uno de ustedes por el buen
trabajo que ustedes están realizando en el área, no te preocupes si tardas más que otros en llegar a la
meta. Dios lo hizo todo hermoso para el momento apropiado.
Ø
Mi estimado estudiante, nuestra mayor
debilidad radica en darse por vencido. La forma más segura de tener éxito es
intentarlo una vez más.
Algunas nociones previas
sobre igualdad y desigualdad
AHORA RESPONDE LAS SIGUIENTES INTERROGANTES:
¿De
qué trata el tema?
……………………………………………………………………
¿Qué es una ecuación de primer
grado?
……………………………………………………………………
¿Qué es una inecuación de
primer grado?
……………………………………………………………………
¿Cuáles son los elementos de
una expresión algebraica?
…………………………………………………………………………
¿QUÉ
APRENDERÉ HOY?
Aprendemos a
reconocer los elementos y propiedades de ecuaciones e inecuaciones de primer
grado a través diagramas para poder desarrollar los problemas.
¿QUÉ
haré?:
Establecerás relaciones de equivalencia y transformaras
en expresiones equivalencias que incluyan ecuaciones lineales e inecuaciones de
primer grado, luego representaras con lenguaje algebraico la comprensión de la
solución de la ecuación e inecuación empleando estrategias heurísticas y
propiedades
¿Qué es
ecuación?
Una ecuación es una igualdad matemática
entre dos expresiones, denominadas miembros y separadas por el signo igual, en
las que aparece elementos conocidos o incógnitas, relacionados mediante
operaciones matemáticas.
Ejemplo:
4x – 2 = 7x + 1
PROPIEDADES DE LA ECUACIÓN DE PRIMER
GRADO
Toda ecuación se transforma en otra equivalente cuando se
ejecutan operaciones elementales iguales en ambos miembros.
PROPIEDADES:
1. Si a los
dos miembros de una ecuación se les suma una misma cantidad positiva o
negativa, se obtiene otra ecuación equivalente a la dada.
2x = 16 4x + 2 = 22
2x - 10
+10 = 16 +10
4x + 2 – 2 = 22 -2
2x = 26
4x = 20
x = 13 x = 5
2.
Si a los dos miembros de una ecuación se
multiplican o se divide por una misma expresión, se
obtiene otra ecuación equivalente a la dada.
SITUACIÓN 1.
La
base de un rectángulo es el doble que la altura ¿cuáles son las dimensiones si
el perímetro mide 54 cm?
SOLUCIÓN
SITUACIÓN
PROBLEMÁTICA 2.
Si la edad de María es el triple que la de
Pepe y dentro de 10 años será el doble. ¿Cuál es la edad actual de Pepe y
María?
SOLUCIÓN
Planteamiento:
Edad
Actual
|
Dentro
de 10 años
|
|
María
|
3x
|
3x
+ 10
|
Pepe
|
x
|
x +10
|
Ecuación: “dentro de 10 años la
edad será el doble”
3x+10 = 2. (x+10)
Resolución:
3x+10 = 2. (x+10)
3x+10 = 2x+20
3x-2x = 20-10
X= 10
¿Qué es una
inecuación lineal o inecuación de primer grado?
Una inecuación lineal o inecuación de primer grado es una
desigualdad algebraica en la que aparecen una o más incógnitas en los miembros
de la desigualdad. El exponente de la variable o incógnita es uno.
Inecuación lineal de la forma:
ax > b, ax < b, ax ≥ b y ax ≤ b; ꓯ a = 0
Propiedades para resolver inecuaciones.
1.
Si a los dos miembros de una inecuación se les suma una
misma cantidad o se le resta un mismo número, la inecuación resultante es
equivalente.
Si: a < b entonces a + c < b + c; ꓯ c ∈ R
Ejemplos:
x +
6 > 16 x – 5 ≤
25
x +
6 – 6 > 16 – 6 x - 5 +5 ≤
25 +5
x > 10
x ≤
20
2.
Si a los dos miembros de una inecuación se le multiplica
o divide por un mismo número positivo, la inecuación resultante es equivalente.
Si: a < b y c > 0 entonces a . c < b . c; ꓯ c ∈ R
Ejemplos:
3. Si a los dos miembros de una inecuación se le multiplica
o divide por un mismo número negativo, la inecuación resultante cambia el sentido
de la desigualdad.
Si: a
< b y c < 0 entonces a . c > b
. c; ꓯ c ∈ R
Ejemplos:
SITUACIÓN PROBLEMÁTICA 1.
María
tiene 15 años menos que Alejandra. Si las edades de ambas, suman menos de 57
años. ¿Cuál es la máxima edad que puede tener María?
Solución
Edad
de Alejandra: x x + x – 15 < 57
2x < 57 + 15
Edad
de María: x – 15
2x < 72
x < 72 : 2
x < 36
situación
problemática 2.
1 semana
|
|
Lucho
|
x – 20
|
Juan
|
x
|
X + x – 20 < 99
2x < 99 + 20
2x < 119
x <
59,5
x = {59;58;57;56,55; …; 21}
Respuesta: Juan
tiene ahorrado como máximo 59 soles.
RETROALIMENTACIÓN:
DESAFIÓ PARA LA CASA:
1.
Completa la tabla con ejemplos relacionado al tema.
Clasificación
de las ecuaciones de primer grado
|
|||
Por su número de
variables
|
1 sola variable
|
2 variable
|
3 variables
|
Por sus
coeficientes
|
entero
|
fraccionario
|
Literales
|
Por su tipo de
solución
|
Compatible: solución única
|
Compatible: infinitas solución
|
Incompatibles: no tiene solución
|
2. Carlos
tienen 3 años y su hermano 8 años. Cuantos años han de pasar para que la edad
del hermano mayor sea el doble que la de Carlos. ¿Cuál es el planteamiento de
la expresión algebraica? y ¿calcule las edades de edad uno?
ME
PREGUNTO:
¿Qué aprendiste
hoy?
¿Qué dificultades haz tenido?
¿Para qué te servirá lo aprendido?
¿En qué otras ocasiones podrías utilizar lo
que has aprendido?
MÁS INFORMACIÓN:
Te invito a ver este link PARA AQUELLOS ESTUDIANTES QUE TIENEN INTERNET
EN CASA
GRACIAS POR SU ATENCIÓN A ESTA CLASE
Estimados estudiantes les dejamos
nuestra dirección para cualquier consulta.
Prof. MAURO CABELLO MELO Celular N° 964836005
Secciones 2° A, B, C, D
Prof. JESSICA RAMOS FLORES Celular N° 992312375
Secciones 2° E, F
SOLUCIONARIO DE LA SESIÓN 22
1.
Qué cantidad de
tela para tapates utilizó la señora Carmen, en un pentágono regular de 6 cm de
lado y 4,1 cm de apotema.
Datos:
Figura: Pentágono
L = 6 cm
ap = 4,1 cm
Para calcular la cantidad de tela que se utilizó para los tapetes, se
debe aplicar la fórmula de Área de polígonos.
a) 61,5 cm2 b)
51,5 cm2 c) 61,9 cm2 d) 61,3 cm2
2.
Calcula el
perímetro y área de un octágono de lado 16 y apotema 19,3 cm.
Datos:
Figura: Octágono
L = 16 cm
ap = 19,3 cm
Para calcular Área y el perímetro, aplicamos las fórmulas de polígonos.
·
Primero calculamos
el perímetro del octágono.
P = 16 . 8
P = 128 cm
·
Luego calculamos el
área del octágono.
a)
128 cm y 1235,2 cm2 c) 128 cm y 1245,2 cm2
b)
128 cm y 1135,2 cm2 d) 128 cm y 1255,2 cm2
3.
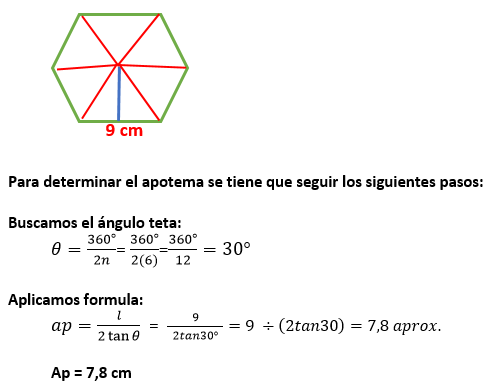
Calcula la apotema
del siguiente polígono que se muestra (seguir los procedimientos explicados)
a)
7, 5 cm b) 7, 6cm c) 7,9 cm d) 7,8 cm
4.
Calcula el
perímetro y el área de un heptágono regular.
b) 49 cm y 176,7 cm2 d) 49 cm y 176,4 cm2







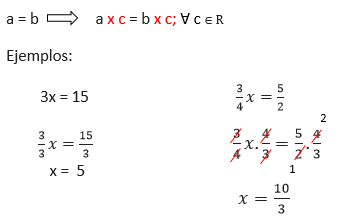







No hay comentarios.:
Publicar un comentario